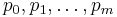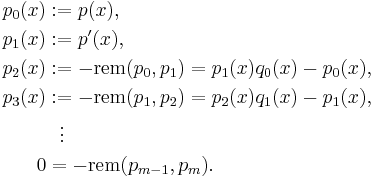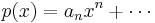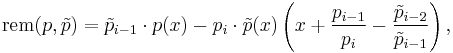Sturm's theorem
In mathematics, Sturm's theorem is a symbolic procedure to determine the number of distinct real roots of a polynomial. It was named for Jacques Charles François Sturm. Whereas the fundamental theorem of algebra readily yields the number of complex roots of a polynomial, counted according to their multiplicities, Sturm's theorem deals with real roots only and disregards their multiplicities.
Contents |
Sturm chains
A Sturm chain or Sturm sequence is a finite sequence of polynomials
of decreasing degree with these following properties:
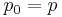 is square free (no square factors, i.e., no repeated roots);
is square free (no square factors, i.e., no repeated roots);- if
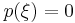 , then
, then 
- if
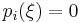 for
for 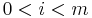 then
then 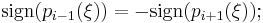
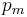 does not change its sign.
does not change its sign.
To obtain a Sturm chain, Sturm himself proposed to choose the intermediary results when applying Euclid's algorithm to p and its derivative:
That is, successively take the remainders with polynomial division and change their signs. Since 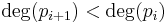 for
for 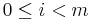 , the algorithm terminates. The final polynomial, pm, is the greatest common divisor of p and its derivative. If p is square free, it shares no roots with its derivative, hence pm will be a non-zero constant polynomial. The Sturm chain, called the canonical Sturm chain, then is
, the algorithm terminates. The final polynomial, pm, is the greatest common divisor of p and its derivative. If p is square free, it shares no roots with its derivative, hence pm will be a non-zero constant polynomial. The Sturm chain, called the canonical Sturm chain, then is
If p is not square-free, this sequence does not formally satisfy the definition of a Sturm chain above, nevertheless it still satisfies the conclusion of Sturm's theorem (see below).
Statement
Let 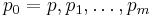 be a Sturm chain, where p is a square-free polynomial, and let σ(ξ) denote the number of sign changes (zeroes are not counted) in the sequence
be a Sturm chain, where p is a square-free polynomial, and let σ(ξ) denote the number of sign changes (zeroes are not counted) in the sequence
Sturm's theorem then states that for two real numbers a < b, the number of distinct roots of p in the half-open interval (a,b] is σ(a) − σ(b).
The non-square-free case
Let 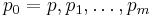 be the canonical Sturm sequence of a polynomial p, not necessarily square-free. Then σ(a) − σ(b) is the number of distinct roots of p in (a,b] whenever a < b are real numbers such that neither a nor b is a multiple root of p.
be the canonical Sturm sequence of a polynomial p, not necessarily square-free. Then σ(a) − σ(b) is the number of distinct roots of p in (a,b] whenever a < b are real numbers such that neither a nor b is a multiple root of p.
Proof
Polynomials are continuous functions, and any sign change must occur at a root, so consider the behavior of a Sturm chain around the roots of its constituent polynomials.
First, note that two adjacent polynomials can share a common root only when it is a multiple root of p (in which case it is a root of every pi). Indeed, if pi and pi−1 are both zero at  , then pi+1 also have to be zero at
, then pi+1 also have to be zero at  , since
, since 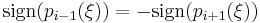 . The zero then propagates recursively up and down the chain, so that
. The zero then propagates recursively up and down the chain, so that  is a root of all the polynomials p0, ..., pm.
is a root of all the polynomials p0, ..., pm.
Next, consider roots of polynomials in the interior (i.e., 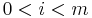 ) of the Sturm chain that are not multiple roots of p. If
) of the Sturm chain that are not multiple roots of p. If 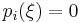 , then we know from the previous paragraph that
, then we know from the previous paragraph that 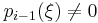 and
and 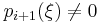 . Furthermore,
. Furthermore, 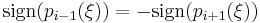 , so in the vicinity of
, so in the vicinity of  we've got a single sign change across pi−1, pi, pi+1. In other words, sign changes in the interior of the Sturm chain do not affect the total number of sign changes across the chain.
we've got a single sign change across pi−1, pi, pi+1. In other words, sign changes in the interior of the Sturm chain do not affect the total number of sign changes across the chain.
So only roots of the original polynomial, at the top of the chain, can affect the total number of sign changes. Consider a root  , so
, so 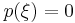 , and assume first that it is a simple root. Then p's derivative, which is p1, must be non-zero at
, and assume first that it is a simple root. Then p's derivative, which is p1, must be non-zero at  , so p must be either increasing or decreasing at
, so p must be either increasing or decreasing at  . If it's increasing, then its sign is changing from negative to positive as we move from left to right while its derivative (again, p1) is positive, so the total number of sign changes decreases by one. Conversely, if it's decreasing, then its sign changes from positive to negative while its derivative is negative, so again the total number of sign changes decreases by one.
. If it's increasing, then its sign is changing from negative to positive as we move from left to right while its derivative (again, p1) is positive, so the total number of sign changes decreases by one. Conversely, if it's decreasing, then its sign changes from positive to negative while its derivative is negative, so again the total number of sign changes decreases by one.
Finally, let  be a multiple root of p, and let p0, ..., pm be the canonical Sturm chain. Let d = gcd(p,p'), q = p/d, and let q0, ..., qm' be the canonical Sturm chain of q. Then m = m' and pi = qid for every i. In particular, σ(x) is the same for both chains whenever x is not a root of d. Then the number of sign changes (in either chain) around
be a multiple root of p, and let p0, ..., pm be the canonical Sturm chain. Let d = gcd(p,p'), q = p/d, and let q0, ..., qm' be the canonical Sturm chain of q. Then m = m' and pi = qid for every i. In particular, σ(x) is the same for both chains whenever x is not a root of d. Then the number of sign changes (in either chain) around  decreases by one, since
decreases by one, since  is a simple root of q.
is a simple root of q.
In summary, only sign changes at roots of the original polynomial affect the total number of sign changes across the chain, and the total number of sign changes always decreases by one as we pass a root. The theorem follows directly.
Applications
Bounds
This can be used to compute the total number of real roots a polynomial has (to use, for example, as an input to a numerical root finder) by choosing a and b appropriately. For example, a bound due to Cauchy says that all real roots of a polynomial with coefficients ai are in the interval [−M, M], where
Alternatively, we can use the fact that for large x, the sign of
is 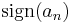 , whereas
, whereas 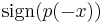 is
is 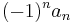 .
.
In this way, simply counting the sign changes in the leading coefficients in the Sturm chain readily gives the number of distinct real roots of a polynomial.
We can also determine the multiplicity of a given root, say ξ, with the help of Sturm's theorem. Indeed, suppose we know a and b bracketing ξ, with σ(a) − σ(b) = 1. Then, ξ has multiplicity k precisely when ξ is a root with multiplicity k − 1 of pm (since it is the GCD of p and its derivative).
Quotient
The remainder is needed to compute the chain using Euclid's algorithm. For two polynomials 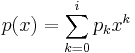 and
and 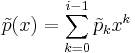 this is accomplished (for non-vanishing
this is accomplished (for non-vanishing 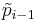 ) by
) by
where the quotient is built solely of the first two leading coefficients.
Generalized Sturm chains
Let ξ be in the compact interval [a,b]. A generalized Sturm chain over [a,b] is a finite sequence of real polynomials (X0,X1,…,Xr) such that:
- X(a)X(b) ≠ 0
- sign(Xr) is constant on [a,b]
- If Xi(ξ) = 0 for 1 ≤ i ≤ r−1, then Xi−1(ξ)Xi+1(ξ) < 0.
One can check that each Sturm chain is indeed a generalized Sturm chain.
See also
- Routh–Hurwitz theorem
- Hurwitz's theorem (complex analysis)
- Descartes' rule of signs
- Rouché's theorem
- Properties of polynomial roots
- Gauss–Lucas theorem
- Turán's inequalities
- D.G. Hook and P.R. McAree, "Using Sturm Sequences To Bracket Real Roots of Polynomial Equations" in Graphic Gems I (A. Glassner ed.), Academic Press, p. 416–422, 1990.
References
- Chee Yap, Fundamental Problems in Algorithmic Algebra, Oxford University Press, 2000. ISBN 0-19-512516-9
External links
- C code from Graphic Gems by D.G. Hook and P.R. McAree.